近日，北京理工大学王涌天、黄玲玲教授团队与香港大学张霜教授合作，提出了一种基于达曼涡旋超表面的光束微分运算方法，实现了数学函数微分加减运算的全光表达。第一作者为维多利亚老品牌vic3308黄玲玲教授团队博士生张雪，王涌天教授、黄玲玲教授和张霜教授为共同通讯作者。该项研究成果发表在国际著名期刊 Science Advances 上，题目为Basis function approach for diffractive pattern generation with Dammann Vortex Metasurfaces。

光学计算是现代信息技术领域的热点研究内容，不同于电子计算起源于对逻辑门的控制，光学计算拥有多重物理属性以及高速并行运算能力。函数微分和四则运算作为数学理论的核心基础，也是提高现代光子计算能力的重要手段。轨道角动量作为光的一种基本物理属性，具备无限数目正交通道的特点，因此应用轨道角动量的复用或解复用可以实现光信息的多路复载。广义涡旋光束能够将不同的轨道角动量与围绕光学奇点相位微分的疏密变化构建关联，实现函数式相位微分与光束轮廓形态的结合，从而打破传统涡旋光束相位微分为常数的限制。通常，达曼涡旋光栅是轨道角动量复用和解复用应用的理论基础，它能够在光栅的不同衍射级次上有序的呈现携带不同拓扑荷数的涡旋光束，而涡旋光束阵列之间存在典型的与衍射级次相关的倍乘与加减运算关系。

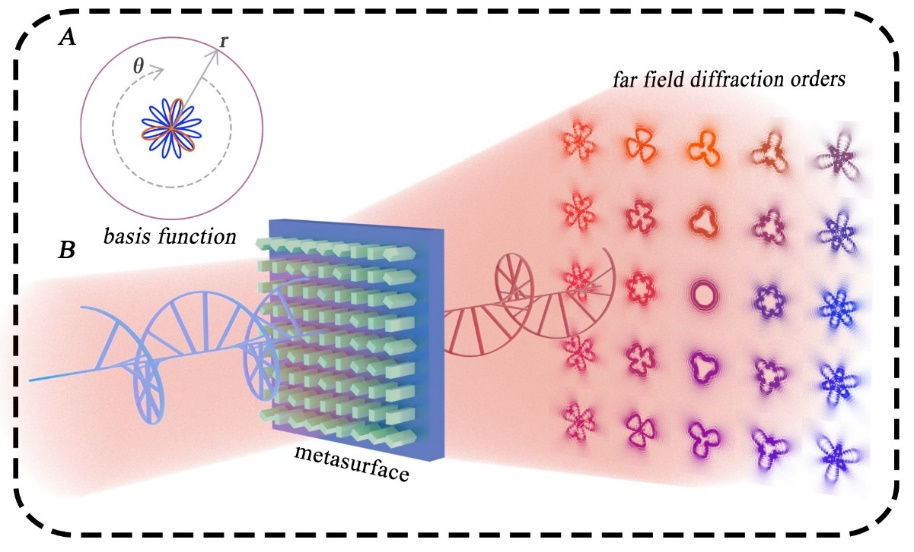
为了利用全光手段实现函数微分和四则运算功能的结合，黄玲玲教授团队应用广义涡旋光束的设计方法，结合达曼涡旋优化，通过设置自定义的相位微分基本函数，实现了不同衍射级次的多种微分函数加减运算的直观光学展现。以三角函数为例，类比于傅里叶级次方法对任意周期函数的展开表达，利用中心基本拓扑荷的相位微分、横向与纵向相位微分函数变化的结合，实现了不同衍射级次上不同函数特征的分布。根据广义涡旋光束相位微分与光束形态之间的关联，不同衍射级次上的各不相同函数变化呈现为不同的光束轮廓，构成了丰富多样的阵列图案，实验验证单次同时计算显示的各不相同涡旋光束阵列可多达7×7。相比于传统光计算，该方法实现了函数微分加减运算的直观图像化表达，并且这种新型的函数式微分加减计算功能突破了传统光学计算围绕特定三角函数数值进行分析的局限。此外，针对单个光束的闭合圆周覆盖连续自变量范围，以及多个光束之间的微分加减运算关联都使得光计算拥有更强的灵活性和功能性。

这种新提出的光束微分运算方法，实现了高速大容量并列计算和直观化显示，利用光束形态如广义涡旋光、结构光、空间模式作为数学运算的展示，打破了传统光计算图形显示的困难，更进一步丰富了光计算的形式与功能。并且这种光学微分运算超表面支持复杂形式光束输入运算，因此对于轨道角动量信息传输与存储加密都能够引入更丰富的自由度。该方法能够为探索涡旋信息加密、光学操纵和光通信、量子纠缠等各种应用打开新的大门。

　　文章链接：https://www.science.org/doi/10.1126/sciadv.abp8073